La Teoria della Relatività

Introduzione

La teoria della relatività, elaborata da Albert Einstein all’inizio del XX secolo, è alla base dell’intera fisica moderna. Solo mediante la teoria della relatività si può dare una sistemazione completa all’elettromagnetismo e alla teoria della gravitazione; ed è solo grazie ad essa che la fisica nucleare e la fisica delle particelle elementari hanno potuto svilupparsi e avere le applicazioni ingegneristiche attuali. La teoria della relatività si può suddividere, anche storicamente, in due “fasi” successive: la relatività speciale e la relatività generale. Il problema di fondo, per risolvere il quale Einstein elaborò la propria teoria, è in ambedue i casi quello di dare una forma invariante, indipendente cioè dal sistema di riferimento, alle leggi fisiche. Per molto tempo si credette che l’unica risoluzione del problema fosse costituita dal “Principio di relatività di Galileo”. Secondo questo principio tutti i sistemi di riferimento “inerziali” sono equivalenti per la descrizione dei fenomeni meccanici. Ricordiamo che un sistema di riferimento è detto “inerziale” se in esso sono soddisfatte le tre leggi di Newton della meccanica. Comunemente si dice che il sistema delle stelle fisse (cioè un sistema avente come origine il centro del Sole e l’orientazione degli assi invariante rispetto alla posizione delle stelle fisse) è inerziale. Un sistema di riferimento solidale con la Terra non è inerziale in quanto la Terra è in moto rotatorio su se stessa. Gli effetti dovuti a questo moto sono però così piccoli che, in prima approssimazione, si possono trascurare e considerare la Terra un sistema di riferimento inerziale. Il principio di relatività venne dedotto da Galileo dallo studio dei fenomeni meccanici noti al suo tempo (basta ricordare il famoso esperimento della caduta dei gravi dalla torre di Pisa). Esso viene messo in discussione alla fine del XIX secolo in seguito alla scoperta dei fenomeni elettromagnetici. In modo particolare la formulazione maxwelliana dell’elettromagnetismo e la scoperta della natura elettromagnetica della luce portavano a contraddizioni molto profonde con il principio di relatività galileiano. Alcuni tra i più famosi fisici dell’epoca, in particolare il francese Jules-Henry Poincarè e l’olandese Hendrik A. Lorentz tentarono di risolvere queste contraddizioni ma con scarsi risultati. Bisogna attendere il 1905, anno in cui viene pubblicato da Albert Einstein (1879 – 1955) sulla rivista “Annalen der physik” il famoso articolo intitolato Electrodynamic bewegter korpen (Sull’elettrodinamica dei corpi in moto) perché si riescano a superare le contraddizioni tra principio di relatività e teoria elettromagnetica. È in questo articolo che Einstein espone i concetti della sua teoria. La teoria della relatività di Einstein si basa su due postulati:

Le leggi della fisica sono le stesse in tutti i sistemi di riferimento inerziali.
La velocità della luce è costante in tutti i sistemi di riferimento.

Egli inoltre analizza a fondo i concetti di spazio e di tempo e dimostra, sulla base di due postulati, che né lo spazio né il tempo hanno carattere assoluto; ogni osservatore ha un suo proprio tempo e un suo proprio sistema di coordinate. Einstein dimostra inoltre, partendo dall’esistenza di un tempo proprio per ogni osservatore, che le trasformazioni di Galileo sono errate. Esse vanno sostituite con leggi di trasformazione più generali, note come “leggi di trasformazione di Lorentz”. Utilizzando queste leggi di trasformazione Einstein dimostra che le equazioni di Maxwell del campo elettromagnetico sono invarianti; non esiste quindi alcuna contraddizione tra principio di relatività ed elettromagnetismo. La teoria della relatività einsteiniana non si limita a spiegare i fatti sperimentali: partendo da essa si derivano una nuova cinematica e una nuova dinamica, chiamate “relativistiche”, che sostituiscono la meccanica newtoniana. La dinamica relativistica è alla base di tutta la moderna ingegneria nucleare. Con la teoria della relatività Einstein stabilisce la completa equivalenza, per quanto riguarda la descrizione dei fenomeni fisici, di tutti i sistemi di riferimento inerziali; così facendo egli estende il principio di Galileo, valido per i soli fenomeni meccanici, a tutta la fisica. La teoria rimane però limitata ai soli sistemi di riferimento inerziali, da cui il nome di “relatività ristretta”. Il desiderio di generalità vorrebbe un principio di relatività valido anche per tutti i sistemi di riferimento, anche non inerziali. È ancora Einstein a risolvere il problema formulando la “teoria della relatività generale” nell’opera “Die Grundlage der aligemeinen Relativitätstheorie“ (I fondamenti della relatività generale), presentata nel 1916. egli dimostra l’equivalenza tra un sistema di riferimento inerziale e uno non inerziale in cui è presente un campo gravitazionale; si può cioè passare da un sistema di riferimento inerziale a uno non inerziale introducendo un opportuno campo gravitazionale. Su queste basi Einstein sviluppa una nuova teoria della gravitazione, che si sostituisce a quella newtoniana e che è alla base di tutta la moderna cosmologia.

Difficoltà della fisica classica

Relatività galileiana:

Per introdurre il concetto di relatività galileiana ci si può servire di un esempio dovuto allo stesso Galileo. Supponiamo che una nave viaggi a velocità costante: dalla cima dell’albero un marinaio lascia cadere un sasso. Per un osservatore sulla nave la traiettoria del sasso è una linea retta parallela all’albero; un osservatore sulla terraferma vede invece cadere il sasso lungo una traiettoria parabolica. È evidente da questo esempio che non esiste una traiettoria assoluta lungo cui si muove il sasso, ma solo una traiettoria relativa per ogni particolare osservatore. Se associamo ad ogni osservatore un sistema di riferimento possiamo dire che “rispetto a un sistema di riferimento rigidamente collegato alla nave il sasso descrive una linea retta, mentre rispetto a un sistema di riferimento rigidamente collegato alla terraferma descrive una parabola”. Consideriamo ancora l’esempio precedente; in entrambi i sistemi di riferimento il sasso inizia il suo moto dalla cima dell’albero e lo termina alla base dell’albero stesso pur percorrendo traiettorie diverse nei due sistemi di riferimento. Da questo fatto possiamo dedurre che le leggi che descrivono il moto del sasso sono le stesse tanto nel sistema di riferimento S (osservatore sulla terraferma) quanto nel sistema di riferimento SI (osservatore sulla nave). Questo risultato particolare può essere esteso a principio generale: ciò venne fatto da Galileo di modo che il principio è noto come “principio di relatività di Galileo”. Esso afferma che le leggi della meccanica sono le stesse in tutti i sistemi di riferimento in moto traslatorio uniforme uno rispetto all’altro. Una conseguenza importante della relatività galileiana, che va sotto il nome di “teorema di addizione della velocità”, è la seguente. Consideriamo ancora la nave dell’esempio precedente e supponiamo che la sua velocità rispetto a un sistema di riferimento connesso con la terraferma sia v0 ; supponiamo inoltre che un marinaio cammini sulla nave, nella direzione del moto, con velocità w0 rispetto a un sistema di riferimento connesso con la nave. Con quale velocità si muove il marinaio per un osservatore sulla terraferma? Se fosse immobile in un intervallo di tempo Δt, percorrerebbe una distanza data da:

Δt × v₀

Durante l’intervallo di tempo Δt, il marinaio avanza di:

Δt × w₀

Quindi egli avanza di:

Δt × (v₀ + w₀)

La sua velocità rispetto a un osservatore sulla terraferma è quindi:

v_t = v₀ + w₀

L’aspetto concettualmente interessante è che la velocità del marinaio è diversa nei due sistemi di riferimento. Generalizzando questo risultato, possiamo dire che la velocità non è invariante: essa assume, in generale, valori diversi passando da un sistema di riferimento a un altro.

L’elettromagnetismo e la relatività galileiana:

La formulazione maxwelliana dell’elettromagnetismo e la scoperta del carattere elettromagnetico della luce posero seriamente in discussione la validità del principio di relatività galileiana. Maxwell aveva dimostrato che la luce è una propagazione ondosa di carattere elettromagnetico. In analogia con i fenomeni ondosi meccanici già noti (ad esempio le onde sonore) sembrava logico supporre l’esistenza di un “mezzo” nel quale si propagasse l’onda elettromagnetica. Che questo mezzo potesse essere una sostanza usuale era da escludere dato che la luce si propaga anche nel vuoto. Si inventò allora una speciale sostanza, l’etere. Le proprietà che doveva possedere questo ipotetico etere erano alquanto strane: doveva essere in grado di penetrare tutti i corpi ed essere capace di trasmettere vibrazioni luminose, che sono trasversali, cioè perpendicolari alla direzione di propagazione, il che è una tipica proprietà dei corpi solidi. Secondo la teoria di Maxwell le equazioni del campo elettromagnetico non sono valide per tutti i sistemi di riferimento, ma solo per quelli immobili rispetto all’etere. Il problema era concettualmente simile a quello risolto da Galileo nell’ambito della meccanica. Contrariamente alle leggi di Newton però le equazioni di Maxwell non sono invarianti per trasformazioni di Galileo; assumono cioè una forma diversa in un sistema di riferimento in moto (anche rettilineo e uniforme) rispetto all’etere. Infatti nelle equazioni di Maxwell compare in modo essenziale la velocità della luce nel vuoto c; poiché la velocità non è invariante per trasformazioni di Galileo anche le equazioni di Maxwell non lo sono. Questo fatto indusse a ritenere possibile di evidenziare sperimentalmente il moto di un osservatore rispetto all’etere mediante lo studio dei fenomeni elettromagnetici; ad esempio studiando come varia la velocità della luce al variare della velocità della sorgente. Secondo la legge di trasformazione galileiana la velocità della luce dovrebbe essere massima quando essa si propaga nella stessa direzione di moto della sorgente e minima quando si propaga nel senso opposto. La più celebre delle esperienze di questo tipo fu quella realizzata da Michelson e Morley tra il 1881 e il 1887.

L’esperimento di Michelson e Morley:

L’idea base dell’esperimento è di confrontare la velocità di percorrenza della luce lungo due cammini perpendicolari, uno dei quali parallelo alla direzione del moto della sorgente. Il problema maggiore che Michelson e Morley dovettero affrontare fu quello di rilevare l’eventuale differenza di velocità nei due sensi. La soluzione trovata fu di far interferire i raggi luminosi; la differente velocità di percorrenza si traduce in una diversità dei cammini ottici e questo provoca un’influenza osservabile nelle figure d’interferenza. L’esperienza eseguita ripetutamente e con estrema precisione in diverse ore del giorno e in tutti i periodi dell’anno diede sempre risultato negativo: la velocità della luce sembrava essere indipendente dalla velocità della sorgente. Generalizzando il risultato dell’esperimento si può dire che la velocità della luce non è influenzata dal moto relativo tra etere e sistema di riferimento in cui si effettuano le misure (in questo caso la Terra). Per spiegare questo fatto nell’ambito della teoria maxwelliana bisogna ammettere che la Terra è immobile rispetto all’etere. Questa ipotesi è però contraddetta da tutta una serie di altri risultati sperimentali secondo i quali la Terra è invece in moto rispetto all’etere. In particolare basta ricordare il fenomeno dell’aberrazione annua delle stelle e l’esperimento di Fizeau. Il fenomeno dell’aberrazione annua delle stelle, scoperto dall’astronomo inglese James Bradley (1693 – 1762) nel 1727, consiste nel fatto che le stelle sembrano descrivere nel corso dell’anno una piccola ellisse. Nell’ambito di una teoria elettromagnetica basata sull’esistenza dell’etere questo fenomeno è spiegabile solo ammettendo che la Terra sia in moto rispetto all’etere. L’esperimento di Fizeau, eseguito per la prima volta nel 1851 dal fisico francese Armand-Hippolyte-Louis Fizeau (1819 – 1896), consiste nello studio della propagazione della luce nei mezzi in movimento. I risultati che Fizeau ottenne sono spiegabili ammettendo che l’etere sia trascinato solo parzialmente dalla Terra di modo che esiste una velocità relativa tra etere e Terra.

Il concetto di tempo nella fisica relativistica

La sincronizzazione degli orologi:

Il concetto di tempo è intuitivo e tutta la nostra esperienza quotidiana ci dice che il tempo scorre. Nasciamo giovani e diventiamo vecchi con il passare del tempo; il sole sorge la mattina e tramonta la sera, che è più tardi della mattina. Un altro concetto intuitivo, legato alla nostra esperienza quotidiana, è quello di simultaneità: in base a esso ci capita sovente di affermare che degli eventi sono avvenuti “contemporaneamente”. Molte volte però noi usiamo la parola “simultaneo” in modo errato. Consideriamo infatti un treno immaginario, enormemente lungo, tanto che dal vagone di testa non si possa vedere il vagone di coda. Quando il treno si ferma due viaggiatori scendono, uno (A) dal vagone di testa l’altro (B) da quello di coda. In che modo possiamo dire se sono scesi simultaneamente?

La risposta più banale è: fornendo a ciascuno un orologio e facendoci poi riferire l’ora in cui sono scesi. Il metodo sembra ragionevole, ma non tiene conto del fatto che un orologio potrebbe ritardare rispetto all’altro. Il problema diviene allora quello di poter “sincronizzare” gli orologi. Alla stessa distanza da A e da B mettiamo una sorgente luminosa S. S emette un raggio luminoso che viaggia sia verso A sia verso B. Ora, per il secondo dei due postulati di Einstein, il raggio luminoso si propagherà con la stessa velocità c sia nella direzione di A sia in quella di B, e quindi giungerà nel medesimo istante in A e in B. Quando la luce arriva ad A e B, entrambi regolano i loro orologi in modo da indicare la stessa ora, ad esempio le 12. In questo modo e solo in questo modo è possibile sincronizzare gli orologi e quindi parlare di simultaneità di due eventi. Il punto fondamentale di questo esempio sta nell’utilizzo del postulato d’invarianza della velocità della luce: senza questa assunzione non si può trovare alcun metodo logicamente corretto per sincronizzare gli orologi e quindi stabilire la simultaneità di due eventi. La domanda che sorge spontanea a questo punto è la seguente: se due eventi A e B sono simultanei per un certo osservatore S , essi risultano simultanei anche per una altro osservatore SI in moto rettilineo uniforme rispetto ad S ?

La relatività della simultaneità:

Consideriamo allora la seguente situazione: abbiamo cioè un treno in moto, con velocità v rispetto a un osservatore S, fermo a terra. Supponiamo che in A e B si accendano due lampade, e che questo avvenga, per l’osservatore S, simultaneamente. Vediamo cosa accade per un osservatore SI solidale con il treno.

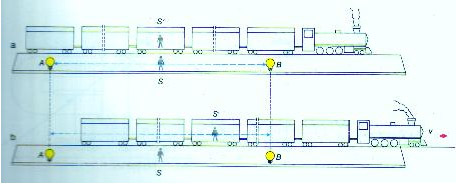
Al momento dell’accensione delle lampade in A e in B i due ipotetici osservatori S e SI si trovano nello stesso punto. Se il treno non si muovesse, i raggi di luce emessi da A e B raggiungerebbero SI simultaneamente. Ma l’osservatore SI si sta muovendo, rispetto ad S, incontro al raggio di luce proveniente da B, mentre sta “sfuggendo” al raggio di luce emesso da A. quindi il raggio di luce emesso da B raggiungerà SI prima di quello emesso da A e quindi per SI l’accensione della lampada in B è avvenuta prima dell’accensione della lampada in A: per SI i due eventi non sono simultanei. Il concetto fondamentale che si ricava dall’esempio riportato è il seguente: gli eventi che sono simultanei per un certo osservatore S non saranno in generale simultanei per un altro osservatore SI, in movimento rispetto ad S. Possiamo quindi affermare che ogni osservatore (sistema di riferimento) ha il suo tempo proprio. Lo specificare un tempo o un dato intervallo di tempo ha significato solo quando venga specificato anche il sistema di riferimento cui ci si riferisce. Questo fatto è assolutamente nuovo nella fisica; prima dell’avvento della teoria della relatività al tempo veniva attribuito un carattere assoluto. Un’ipotesi del genere è però incompatibile con la più naturale definizione di simultaneità, come abbiamo visto nell’esempio precedente. Se abbandoniamo l’ipotesi del tempo assoluto, scompare anche l’incongruenza tra leggi di Maxwell e principio di relatività. Tale apparente incongruenza era legata alla legge di composizione della velocità; questa legge si basa però sulle trasformazioni di Galileo in cui il tempo è assunto essere lo stesso nei due sistemi di riferimento. Poiché questa ipotesi non è sostenibile, anche le trasformazioni di Galileo devono essere abbandonate. In che modo è allora possibile determinare il tempo e la posizione di un evento, rispetto a un osservatore SI, quando conosciamo il tempo o la posizione dello stesso evento rispetto a un osservatore S, in moto relativo rispetto ad SI ? Bisogna trovare delle nuove leggi di trasformazione: queste leggi dovranno essere in accordo con i due postulati della teoria della relatività: in particolare dovranno essere tali per cui la velocità della luce nel vuoto rimanga la stessa per tutti gli osservatori, quale che sia il loro stato di moto.

La massa è energia:

Einstein, tramite i suoi numerosi studi, arrivò ad affermare che la massa è una forma di energia, in quanto essa scompare (secondo una precisa relazione) quando compare energia e viceversa. Tutte le trasformazioni di massa in energia e di energia in massa sono regolate dalla relazione di Einstein che, di solito, è scritta nella forma

E = mc²

In particolare, da questa formula di deduce che un corpo fermo e non soggetto a forze possiede un’energia E0 per il solo fatto di avere una massa m0; tale energia si chiama energia di quiete o di riposo del corpo:

E₀ = m₀c²

Questa relazione è confermata negli esperimenti sulle particelle elementari, dove è possibile osservare la “materializzazione” di particelle a spese della scomparsa di energia e, viceversa, l’annichilazione di due particelle con conseguente emissione della quantità di energia prevista dalla relazione di Einstein.

La teoria della relatività generale

Il numero 49 degli Annalen der physiken pubblicato nel 1916, riporta a pagina 769 un articolo firmato da Albert Einstein che enuncia i “fondamenti della Teoria Generale della Relatività”. La rivoluzione scientifica più importante del secolo scorso, e forse la più significativa in assoluto si compiva senza nessuno strumento scientifico al di fuori del formalismo matematico. La reazione della maggioranza dei fisici fu di incredulità e molti espressero il loro disappunto per una teoria che non poteva essere capita: l’analisi tensoriale, cioè il linguaggio matematico, con cui è scritta la teoria della relatività generale, poteva infatti venir capito solo da un ristretto gruppo di fisici e astronomi.

Il principio di equivalenza:

Il lavoro di Einstein si basa inizialmente sulla sua osservazione del significato profondo del principio di equivalenza. Tale principio enuncia l’esatta equivalenza tra la massa gravitazionale e la massa inerziale. La prima è la responsabile della creazione del campo gravitazionale come descritto dalla teoria di Newton, la seconda è la misura della reazione di un corpo all’azione di una forza su di esso. La loro equivalenza rende possibile il fatto che due palline di diversa massa cadano nello stesso modo se lasciate cadere dalla Torre pendente di Pisa (come pare abbia fatto Galileo): infatti, se la forza con cui la gravità terrestre attira una palla è di massa uguale a y, la forza con cui la gravità attirerà un’altra palla di massa X (con X pari al doppio di x) sarà esattamente pari al doppio di y; in tal modo l’accelerazione con cui le due palline cadono è identica: esse, perciò, atterreranno nello stesso istante. Tale fu l’osservazione, di Galileo, che venne enunciata come principio da Newton che Einstein stravolge con un esperimento ideale, tale cioè da non poter essere compiuto realmente bensì solamente immaginato. Lo strumento preferito da Einstein sono gli ascensori immaginari, cioè ambienti chiusi dove lo sperimentatore non si accorge di quello che succede fuori.

L’ascensore immaginario:

Proviamo a immaginare la sensazione che una persona prova in un ascensore fermo nelle vicinanze di un pianeta in presenza di gravità: l’osservatore ideale chiuso lì dentro vedrà le palline accelerare verso il pavimento dell’ascensore, tutte con la stessa accelerazione g, in modo indipendente dalla loro massa. È esattamente ciò che osserva una persona chiusa in un ascensore identico che viene trascinato nello spazio vuoto con un’accelerazione pari a g. Non c’è modo alcuno di capire se l’accelerazione delle palline è vera o generata dalla gravità! Allo stesso modo possiamo immaginare di essere chiusi nell’ascensore fermi nello spazio vuoto: tutte le palline che utilizziamo per il nostro esperimento rimarranno ferme a mezz’aria o si muoveranno di moto rettilineo uniforme: saremo cioè in un sistema di riferimento inerziale, dove valgono le leggi e le trasformazioni della relatività. Einstein stava proprio cercando di estendere la legge di relatività a tutti i sistemi di riferimento, senza limitarsi a quelli inerziali. Immaginiamo ora di trovarci in un ascensore chiuso che sta cadendo verso la superficie di un pianeta che genera un campo gravitazionale attorno a sé. Prima dell’inevitabile impatto le palline che lasceremo andare dentro l’ascensore rimarranno ferme a mezz’aria o si muoveranno di moto rettilineo a velocità uniforme: non ci accorgeremo cioè di cadere in un campo gravitazionale e potremo benissimo pensare di essere fermi nello spazio vuoto! Nessuna differenza! Prima dell’impatto, però. Un’osservazione più precisa ci farà notare che la pallina, che prima si allontanava da noi a velocità costante verso l’alto, dopo un certo tempo subisce un’accelerazione che la distanzia da noi più velocemente. Ciò significa che l’ascensore in cui siamo deve essere idealmente vasto da permetterci di misurare la differenza dell’accelerazione (o della forza) di gravità tra posizione della pallina e la nostra posizione, ora che ci troviamo fatalmente più vicini alla superficie del pianeta. Ecco la formulazione del principio di equivalenza come ipotizzato da Einstein: in ogni punto dello spazio-tempo, anche se immerso in un campo gravitazionale, è possibile trovare un sistema di riferimento localmente inerziale, dove per localmente si intende non così tanto esteso spazialmente o nel tempo da indurci a notare le differenze del campo gravitazionale tra un punto e l’altro. Tale sistema di riferimento è quello in cui ci troveremmo in caduta libera nel campo gravitazionale, ed in tale riferimento valgono le leggi della relatività speciale. In seguito a questa intuizione Einstein applicò il formalismo dell’analisi tensoriale per cercare il significato profondo alla gravitazione: essa non è una forza, come può essere quella elettrica, ma una proprietà dello spazio-tempo. In parole semplici la materia incurva lo spazio-tempo, in termini matematici il tensore energia-momento modifica il tensore della metrica. Nello spazio-tempo curvo tutti i corpi sono costretti a non muoversi in linea retta, cadendo al suolo in traiettorie paraboliche, o compiendo orbite ellittiche attorno a una stella. Semplicemente, i corpi cadono seguendo le traiettorie più brevi possibili per quello specifico spazio-tempo curvo. Tali traiettorie vengono chiamate geodetiche. Le geodetiche nello spazio-tempo euclideo, cioè quello in cui siamo abituati a vivere e pensare, sono le linee rette. Per andare da un punto ad un altro la via più breve è sempre la retta che congiunge i due punti. E la linea retta, cioè la traiettoria migliore, è unica una volta scelti i due punti di partenza e di arrivo. In questa geometria euclidea le rette parallele non si incontrano mai (se non all’infinito che però è un posto a cui non si può mai arrivare) e la somma degli angoli interni di un triangolo è sempre di 180 gradi. Uno spazio che possieda queste caratteristiche è detto, oltre che euclideo, anche piatto, e corrisponde nella realtà e zone di Universo lontanissime da ogni tipo di materia e di energia. È chiaro che non appena succede qualcosa di notevole nell’Universo si è in presenza di materia (o energia, che secondo la relatività speciale è esattamente la stessa cosa e lo spazio-tempo diventa subito curvo: lo spazio-tempo piatto è solo una comoda approssimazione che possiamo fare in piccole regioni di spazio, dove la gravità non varia apprezzabilmente. Una piccola porzione della superficie terrestre, come la stanza di un laboratorio, o le strade di una città, sono sufficientemente piatte da permetterci di utilizzare una geometria piatta, risparmiandoci in tal modo di dover fare complicati (impossibili) calcoli tensoriali in quattro dimensioni per scegliere il tram giusto per arrivare in tempo al cinema.

Prove sperimentali:

Lo stesso sistema solare è distribuito su di una così vasta regione di Universo che la geometria è quasi sempre euclidea. Solo nelle immediate vicinanze del Sole il campo gravitazionale è intenso a sufficienza da far notare gli effetti dello spazio-tempo curvo: è proprio in questa zona che le prime due prove sperimentali per controllare l’esattezza della teoria della relatività speciale sono state fatte. La prima ipotesi di Einstein riguardava i raggi di luce: anche la luce, che è solo energia, risente della curvatura dello spazio-tempo e compie traiettorie curve. Senza andare in prima persona troppo vicino al Sole osservando la posizione delle stelle prossime al bordo del disco solare (durante un’eclisse totale di Sole, altrimenti la misura sarebbe stata impossibile) l’astrofisico Eddington misurò uno spostamento pari a quello predetto da Einstein. Oggi il fenomeno è osservato su grande scala e non infrequentemente nelle lenti gravitazionali: grandi masse, come gli ammassi di galassie, curvano i raggi luminosi di oggetti lontanissimi posti dietro di essi permettendoci di osservare le galassie nelle loro prime fasi di vita, ovvero singole galassia sdoppiano o moltiplicano le immagini di quasar posti fortuitamente dietro di loro lungo la nostra linea di vista. Einstein calcolò inoltre che in una campo gravitazionale intenso le orbite non dovessero essere ellissi perfette: gli oggetti avrebbero infatti spiraleggiato attorno al massiccio astro centrale, compiendo orbite quasi ellittiche ma non fisse nello spazio, con la direzione del perielio che ruota lentamente. Nel nostro Sistema Solare il campo gravitazionale del Sole è così poco intenso che solo il pianeta più vicino, Mercurio, risente in maniera apprezzabile e misurabile di questo effetto, che venne misurato e trovato esattamente uguale al valore previsto dalla relatività generale. Un’ultima previsione effettuata dallo stesso Einstein fu quella del rallentamento degli orologi, ovvero di una dilatazione del tempo, in presenza di una campo gravitazionale: la scarsa entità del fenomeno e la difficoltà delle misure ritardò notevolmente l’osservazione di questo fenomeno ed Einstein morì prima che, nel 1960, utilizzando radiazioni gamma inviate a Terra da un’altezza di 23 metri, si misurasse il rallentamento della frequenza. Dal 1976, con l’utilizzo di precisissimi orologi atomici, si può percepire la differenza dello scorrere del tempo sulla superficie terrestre e su un aereo in alta quota. Oggi siamo in grado di sapere se l’orologio in esame si trova al piano terra o in cima a un grattacielo, ma gli effetti più impressionanti di questo rallentamento gravitazionale sono stati osservati in quel laboratorio incredibile che è il nostro universo. Le stelle di neutroni sono talmente dense che attorno a loro il campo gravitazionale è così forte da far procedere il perielio di un oggetto orbitante 30.000 volte più velocemente che il Sole con il pianeta Mercurio. I buchi neri riescono a far rallentare il tempo fino a fermarlo: il solito ipotetico osservatore che sta guardando un’astronave o una stella cadere in un buco nero la vedrebbe rallentare fino a non raggiungere mai il confine del buco nero! Colui che sta cadendo nel suo sistema di riferimento in caduta libera – e quindi localmente inerziale – non si accorge invece di niente ed entra nel buco nero. Certo si tratta di una pura ipotesi teorica, perché, nella realtà, sappiamo che le forze gravitazionali di marea nelle vicinanze di una buco nero distruggono qualsiasi cosa. La conferma sperimentale delle teorie di Einstein si è avuta in un tempo relativamente posteriore alla formulazione delle stesse. Ciò si verifica piuttosto spesso nelle moderne discipline scientifiche , all’interno delle quali si elaborano sovente teorie e ipotesi tra loro a volte assai divergenti.

Introduzione

Difficoltà della fisica classica

Il principio di relatività di Einstein

Il concetto di tempo nella fisica relativistica

La teoria della relatività generale